Aptus is very selective about who joins our team because we want to make sure that our team members are well-rounded and brilliant problem solvers, and of course that it's a great culture fit. We have a few questions that we love to ask during the technical interview to gauge the approaches people take to solving problems.

My favorite question by far is the foxhole problem. I guess we can't use it anymore because of this article, but I love it so much and have spent so much time thinking up variations of the problem that I decided to write about it!

What is the Foxhole Problem?

Let's say you are a farmer and you have five fields of crops you are trying to grow. Unfortunately for you, there is a pesky fox which has made a hole in front of each of your fields, so you need to catch it so your crops can grow!

Here are the rules for catching the fox:

• The fox starts in a random hole
• Each morning you can setup a cage outside of one of the holes.
• That evening, you go and check your cage to see if you caught the fox.
• If the fox was in the hole, you trapped and it will get stuck in the cage. You can then move it safely off your property
• If the fox wasn't in that hole, during the night the fox will move to a hole adjacent to the one it is currently in to sleep. For example, if the fox was in hole 2, it will move to hole 1 or 3. If it was in hole 5, the fox must be in hole 4 the next day. (The holes don't wrap)
• The next day you can set your cage up in front of any hole and try again.

Given these rules, is it possible to always catch the fox, and if so, how do you do it?

Initial Approaches

Although it seems very easy, this problem is deceptively difficult once you jump into it. Let's look at some common first approaches.

Repeated Checking

The first approach many take is to just check the middle hole over and over. If you think about it, the fox must wander into the middle hole at some point. So checking that hole repeatedly surely will lead to success eventually. The problem with this approach is the fox could just jump back and forth between the first and second holes or the fourth and fifth holes and you will never catch it in those cases. So if we want a method which will guarantee we catch the fox, we'll have to think of something smarter.

"Sweep"

A common approach taken by many is to sweep across the fields. Maybe on the first day you check hole 1, and then on the next day you check hole 2, all the way down to hole 5. You will quickly realize though that the fox can jump past you! If you check hole 1 on the first day, if the fox was in hole 2, it will now be on the other side of your sweep.

Simplify

Another approach is to try and solve the problem if there were less holes. If there was only 1 hole, the solution is trivial. If there are 2 or 3 holes the solution is also pretty trivial (just check hole 2 twice in a row). It gets quite a bit harder when there are 4 holes. And if you are able to solve it for 4 holes, it's not super clear how to extend it to 5 holes.

Brute Force Solution

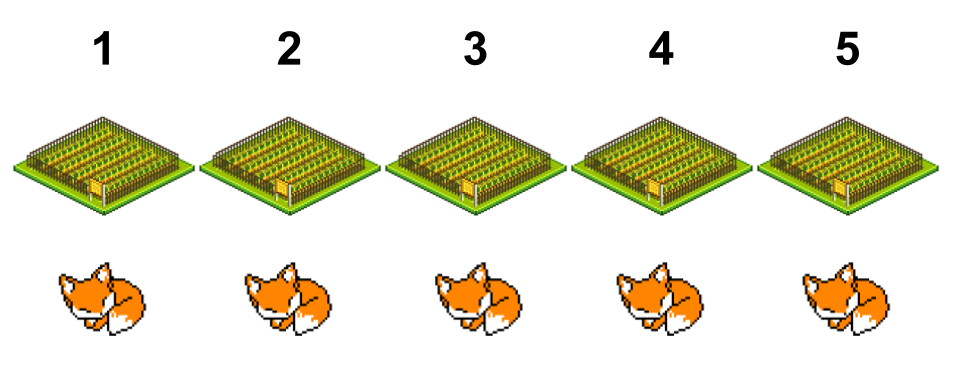
Clearly this problem will require a little more work than those first approaches gave. A good place to start would be to create a system to indicate whether or not we are making progress. A simple system would be to keep track of all the holes a fox could be in each day and just track how that changes as you check holes. The only way for us to guarantee that we catch the fox is for the fox to only have 1 possible hole to be in and we check that hole in the morning. Let's walk through a quick example. At the beginning, the fox can be in any of the 5 holes. We'll indicate this by putting the fox below each field.

Now let's check some hole and see what happens. I'll indicate this by placing an X over the hole I checked, and then showing where the fox could move to on the next day below. In this example I'll check hole 3.

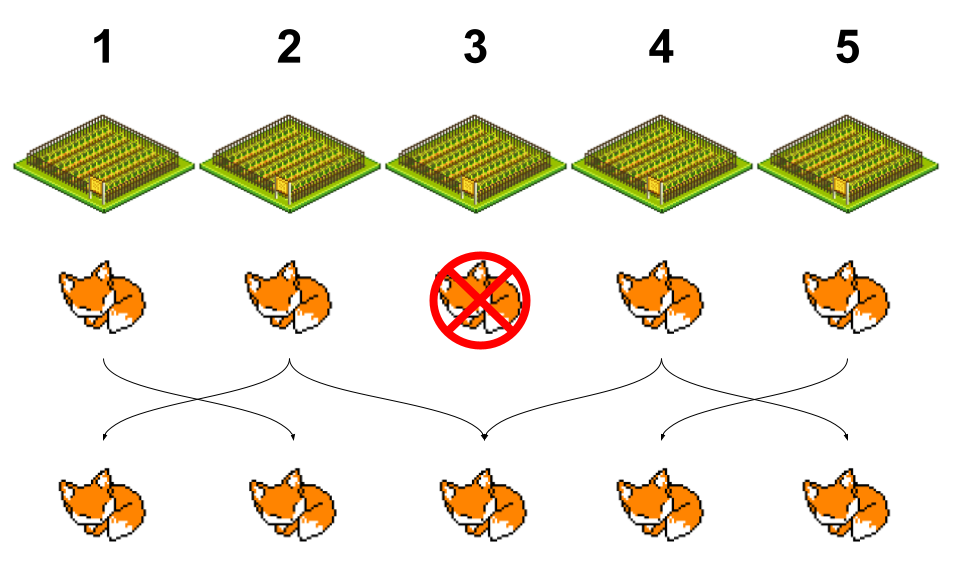
As you can see, after checking hole 3, the fox can still be anywhere. This means the scenario on the second day would be the same as the scenario on the first day. We have not learned anything by doing this. That means we now know there is no solution to this problem which starts by checking hole 3.

There is a way to solve this problem by just brute forcing all possible sequences of checks and just stopping when you either have caught the fox or have reached a scenario which you've already checked (that's what we just did above). This is a very useful way to start solving the problem and is likely the way most people will reach a solution at first.

Insightful Solution

Although most people will solve this problem first by using some brute force method, there are some major insights you could make which vastly simplify the problem. The biggest insight is noticing that if the fox is in an odd hole one day, it must be in an even hole the next day. Similarly if the fox is in an even hole one day, it must be in an odd hole the next day. What this means is that if you can guarantee that you can catch a fox which is in an even hole, you can guarantee you can catch the fox in any hole! This is because if you assume the fox is in an even hole to start and you do not catch it, that means the fox must have started in an odd hole. So you just wait for the fox that started in an odd hole to be in an even hole and you execute your even holed solution!

Even Fox

So let's develop a method for catching a fox in an even hole and show how this works.

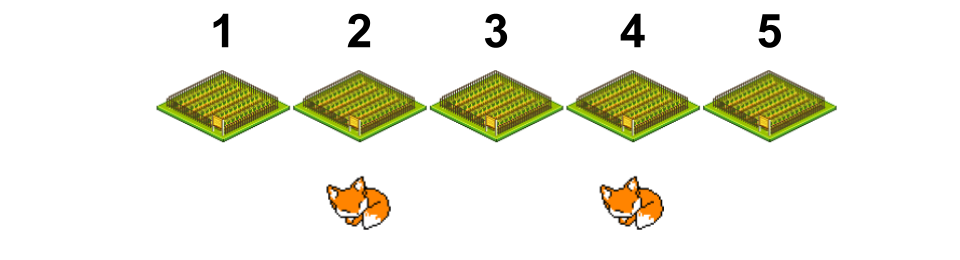
This solution is already more simple than the previous ones. Only 2 foxes to keep track of right off the bat and even better, we don't even have to make a choice about which hole to check because the situation is symmetric. Let's just check hole 2 now!

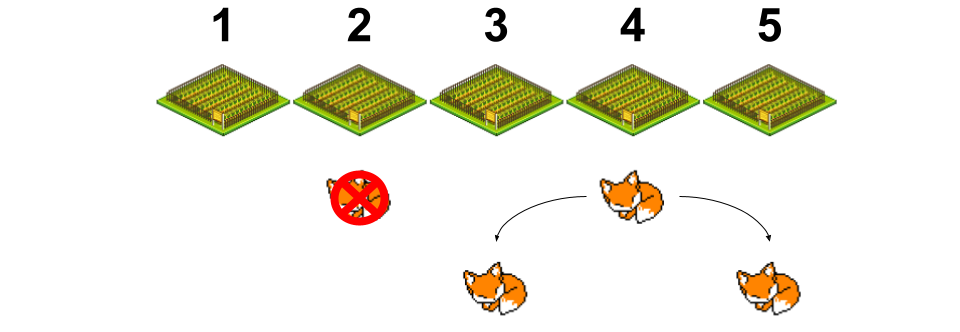
Now we have a big decision to make. If we can realize that if the fox is in hole 5 now, it only has one place to go on the next day, hole 4. However, if it is in hole 3 now, it could either go to hole 2 or hole 4 tomorrow. Therefor, the only logical choice in this situation is to check hole 3. So let's do it and see what happens.

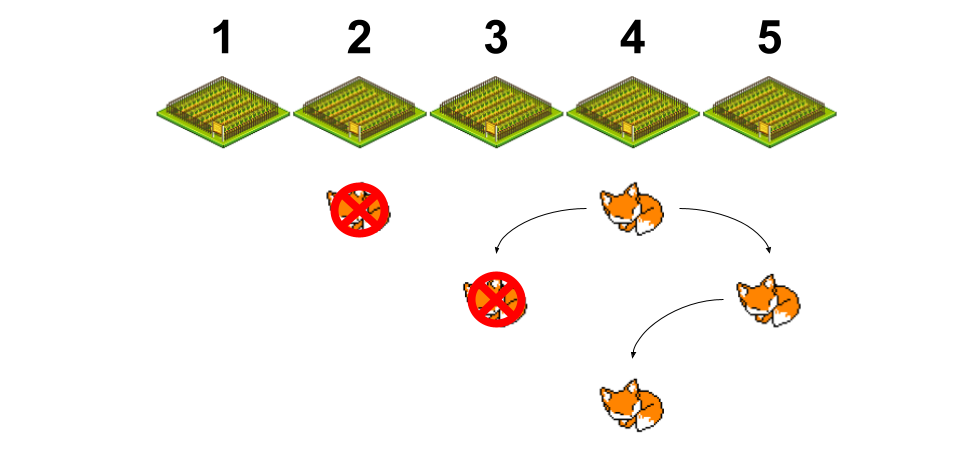
As expected, the fox only has one place to go the next day, and that's hole 4. So we can set our cage up outside of hole 4 and we know we've caught the fox!

Solution

Now that we have a method of catching the even fox (Checking the holes 2 -> 3 -> 4 in that order), let's piece everything together to find a full solution to the problem.

If we check hole 2, then 3, then 4 and we have not caught the fox yet, then we know the fox started on an odd hole. Because if it had started on an even hole we would've caught it. So a logical question to ask next is, where is the fox that started on an odd hole now? Well, on day 1 it was in an odd hole, day 2 and even hole, day 3 an odd hole, and now on day 4 it must be in an even hole.

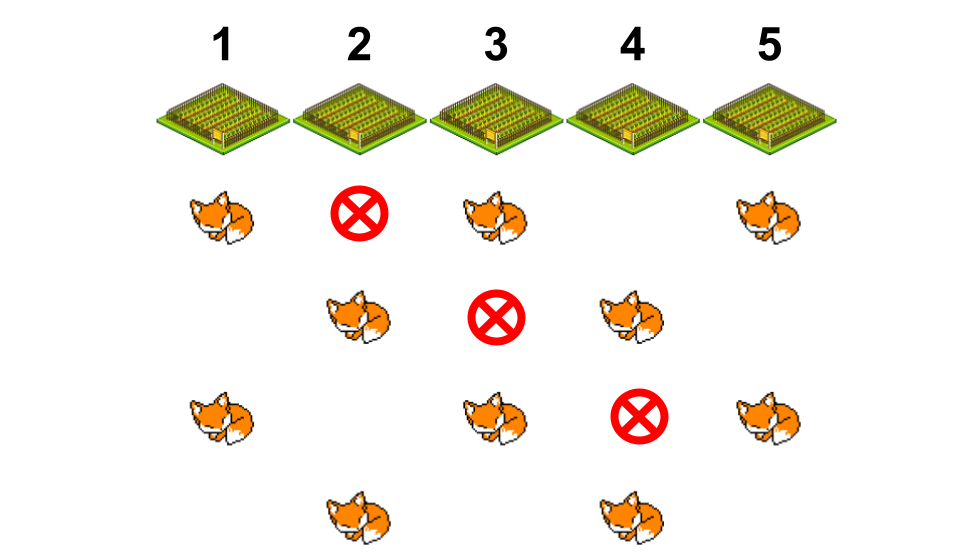
This is amazing news for us, because we know how to catch a fox that's on an even hole! If we just repeat our steps (2 -> 3 -> 4) we will catch the fox. This means that if we check holes in this order 2 -> 3 -> 4 -> 2 -> 3 -> 4 we will always catch the fox.

Extensions

N-Holes

A natural question to ask is can you catch the fox with any number of holes? Say if there were 24 holes, is there still a way to catch the fox? The answer is yes, but I'll leave it as an exercise to the reader to determine what the general solution is for N holes.

Multi-Dimensional

I thought the solution for N-Holes was a bit to simple. So asked myself, what if the fox could move around in a square.

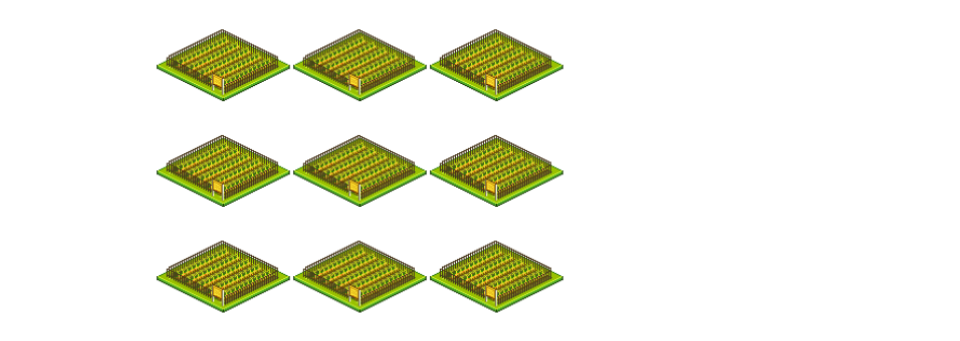
In this case the fox would be allowed to move left and right or up and down. In a grid like this, could you still catch the fox? If you could not catch the fox with just 1 cage, how many cages would you need? What if the foxes could move around in a 3-Dimensional grid, or even a 4-Dimensional grid?

These are the sorts of questions are valuable to ask, especially for developers. Simply solving the problem is never the ending point. If you had taken the brute force solution to this problem, and then stopped, you would not have seen how beautiful the solution could be if you thought about it a bit differently. Imagine what the solution to the original problem will feel like when you gain insights from solving the N-Hole solution, or a multidimensional solution! That should be the goal for everyone. Don't just find the answers, find the beauty in them.

If you enjoyed this problem and are interested in joining our Aptus team, we'd love to hear from you! We're always looking for like-minded individuals to join our team and become one of our developers. Send over your resume and portfolio to career@aptusai.com and mention the foxhole problem.

Or if you're looking for a technology partner who focuses on developing solutions to your problems instead of trying to fit your problems to a solution, let us know! We'd love to hear your ideas and work together!

Contact Lindsay at lindsay.s@aptusai.com to schedule a free business impact consultation!